
- Chi square distribution degrees of freedom how to#
- Chi square distribution degrees of freedom pdf#
- Chi square distribution degrees of freedom professional#
Then, the probability density function of $Y$ isį_Y(y) = \frac \. Theorem: Let $Y$ be a random variable following a chi-squared distribution: Thus, for a chi-square distribution, the mean equals the number of degrees of freedom and the variance equals the twice the number of dgrees of freedom. We can use the Chi-Square distribution to construct confidence intervals for the standard deviation of normally distributed data.Index: The Book of Statistical Proofs ▷ Probability Distributions ▷ Univariate continuous distributions ▷ Chi-squared distribution ▷ Probability density function In fact, the mean of the Chi-Square distribution is equal to the degrees of freedom. Since we are adding up the squared values of k draws from a random normal distribution, the bulk of our values will now cluster around higher values of q (οr χ). Chi-Square Test Properties The variance equals two times the number of degrees of freedom The degree of freedom number is equal to the mean distribution. Plot made available by user Geek3 under on Wikipedia The degrees of freedom (df) is equal to 24,because df n - 1 25 - 1 24.

Note: Here we are using the greek letter χ, which looks confusingly similar to x. This makes a chi2 distribution a gamma distribution with theta2 and alphar/2, where r is the number of degrees of freedom.
Chi square distribution degrees of freedom pdf#
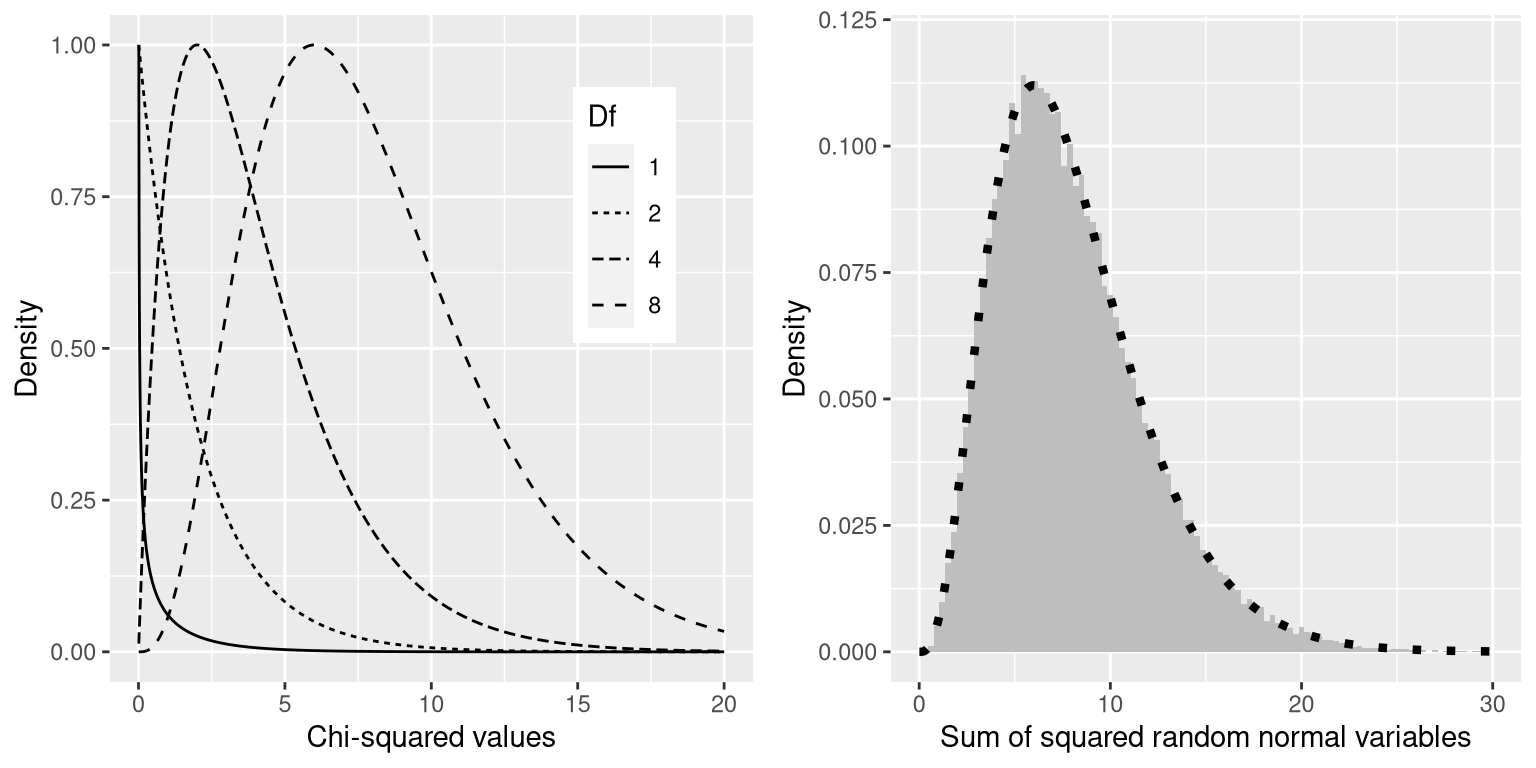
In the following plot, you see how the pdf of the Chi-Square distribution changes based on the degrees of freedom. If Yi have normal independent distributions with mean 0 and variance 1, then chi2sum(i1)rYi2 (1) is distributed as chi2 with r degrees of freedom.
Chi square distribution degrees of freedom professional#
A professional statistician might disagree with it. In a chi-square analysis, the p-value is the probability of obtaining a chi-square as large or larger than that in the current experiment and yet the data will. Please note that this is by no means a rigorous definition. Rather, the summed area of the 'range' of. It is important to remind ourselves that in probability 'density' function graph y-axis does not represent a probability for each variable. The more variables you add, the more variability you introduce, and thus the more degrees of freedom you have. The Chi-square graph in the video plots probability density function value (y-axis) against for chi-squared variable (x-axis) at different degree-of-freedom values.

But as the name implies, you can think of it as the number of variables that can vary. There isn’t a clear-cut definition of degrees of freedom. The number of independent random variables that go into the Chi-Square distribution is known as the degrees of freedom (df). Q_k = X_1^2 + X_2^2 +.+X_k^2 What are Degrees of Freedom? The mean of the chi square distribution is the degree of freedom and the standard devi- ation is twice the degrees of freedom. The degrees of freedom of the Chi Square distribution are equal to the number of standard normal deviates being summed (which is 12 in this case). Thus, you can get to the simplest form of the Chi-Square distribution from a standard normal random variable X by simply squaring X. In a nutshell, the Chi-Square distribution models the distribution of the sum of squares of several independent standard normal random variables. You report your results: The participants’ mean daily calcium intake did not differ from the recommended amount of 1000 mg, t (9) 1.41, p 0.19. In probability theory and statistics, the chi-squared distribution (also chi-square or 2-distribution) with k degrees of freedom is the distribution of a. In the context of confidence intervals, we can measure the difference between a population standard deviation and a sample standard deviation using the Chi-Square distribution. df 9 You calculate a t value of 1.41 for the sample, which corresponds to a p value of. A chi-square variable with one degree of freedom is equal to the square of the standard normal variable. This is more than what you want by pchisq (1,3) so you just need to take the difference. This measurement is quantified using degrees of freedom. chi (Greek ) is pronounced ki as in kind. 1 Answer Sorted by: 6 The pchisq function (whose help is on the same page as dchisq) gives the area to the left (or right with the right argument) of a value, in other words/symbols pchisq (4,3) would give P ( X < 4) for a chisquare with 3 degrees of freedom. The Chi-Square distribution is commonly used to measure how well an observed distribution fits a theoretical one.
Chi square distribution degrees of freedom how to#
If you want to know how to perform chi-square testing for independence or goodness of fit, check out this post.įor those interested, the last section discusses the relationship between the chi-square and the gamma distribution. The chi-squared distribution is implemented in the Wolfram Language as ChiSquareDistribution n.
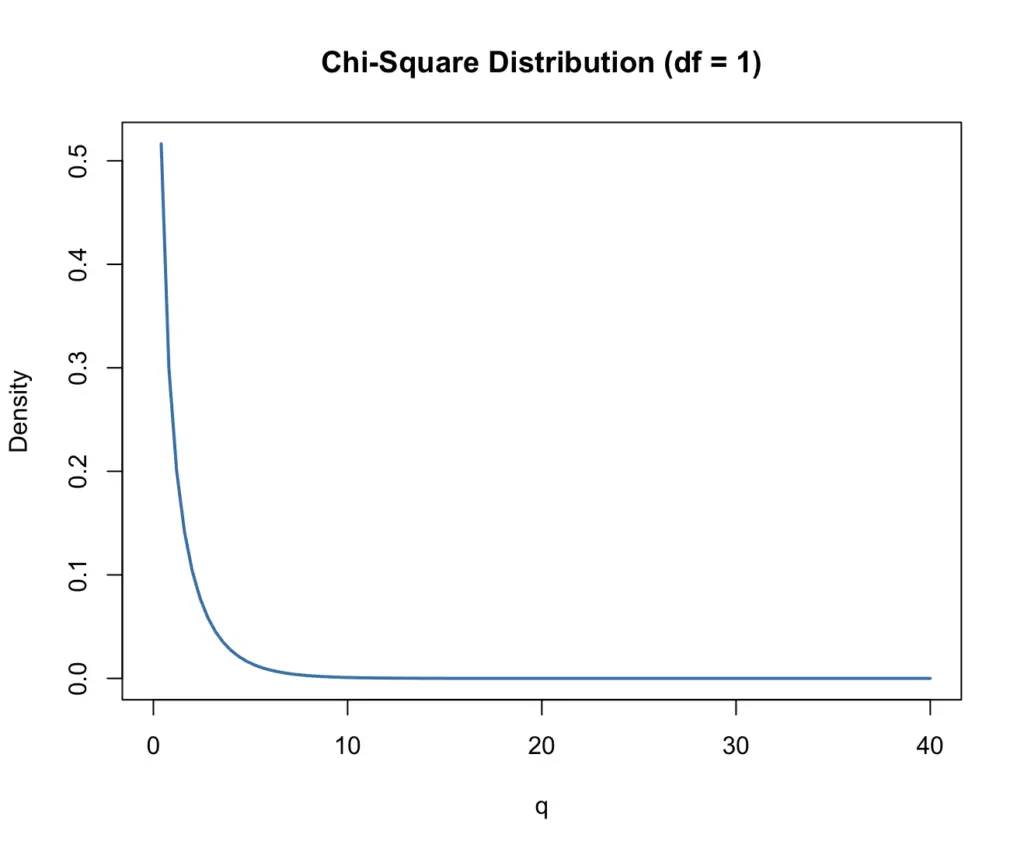
learn how to construct Chi-Square confidence intervals.


 0 kommentar(er)
0 kommentar(er)
